Vector geometry is a first class citizen in Scriptographer. It is a great advantage to understand its basic principles when learning to write scripts for it. After all, there is a reason why the word Vector is used to describe Illustrator's drawing techniques as Vector Graphics.

While building Scriptographer we found vector geometry to be a powerful way of working with positions, movement and paths. Once understood, it proves to be a lot more intuitive and flexible than working with the x- and y- values of the coordinate system directly, as most other visually oriented programming environments do.

As an example of the elegance of vector geometry, here a video that shows the Brush.js script in action. With only 24 lines of code, it produces a mouse tool that acts like a brush, with a variable thickness depending on speed and a sense of a natural expression.

This script is developed step by step in the tutorial Working with Mouse Vectors, along with explanations about each line of code. But before looking at such an applied example, it is crucial to understand the basic principles of vector geometry outlined here.

Points and Vectors

In many ways, vectors are very similar to points. Both are represented by x and a y coordinates. But while points describe absolute positions, vectors represent a relative information; a way to get from one point to another. Here a step-by-step example that explains the relation between vectors and points.

We start by creating two Point objects to describe two absolute locations in the document, defined by their coordinate values:

var point1 = new Point(50, 50);
var point2 = new Point(110, 200);

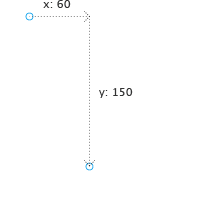
In order to get from point1 to point2, we can say we need to move 60 to the right (in x-direction), and 150 down (in y-direction). These values are the result of subtracting the x- and y-coordinates of point1 from the ones of point2:

var x = point2.x - point1.x;
// = 110 - 50 = 60
var y = point2.y - point1.y;
// = 200 - 50 = 150;

In other words, by adding these two values to the coordinates of point1, we end up at point2.

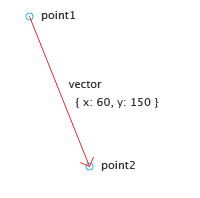
Instead of using these two separate values, it is much easier to use a vector as a container for the them. To calculate this vector, we can simply subtract point1 from point2 instead of the two separate subtractions in the previous step:

var vector = point2 - point1;
// = { x: 110, y: 200 } - { x: 50, y: 50 }
// = { x: 60, y: 150 }

Please note:

Read more about mathematical operations in the Point, Size and Rectangle tutorial.

The result of this subtraction (vector) is still a Point object. Technically, there is no distinction between points and vectors. It is just their meaning that changes: A point is absolute, a vector is relative.

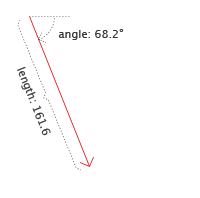
Vectors can also be described as arrows. Similar to arrows, they point in a certain direction, and also indicate an amount of distance to move in that direction. An alternative and often more useful way of describing a vector is therefore by angle and length.

The Point object exposes this alternative notation through the point.angle and point.length properties, which both can be modified too.

print(vector.length);
// 161.55494
print(vector.angle);
// 68.19859

Please note:

By default, all angles in Scriptographer are measured in degrees. Read more about angles and rotation in the chapter about Rotating Vectors.

It is so important that we repeat it again: Vectors contain relative information. All a vector tells us is in which direction and how far to move.

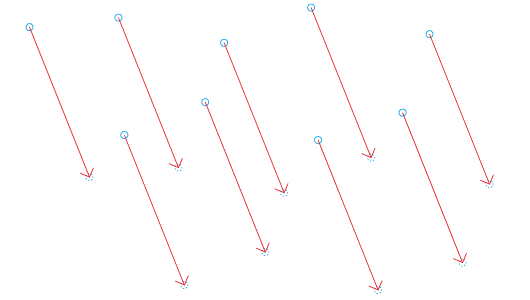
The easiest use of such a vector is to add it to an absolute position of a point. The result will again be an absolute point, which will be at a position shifted from the originating point by the amount specified by the vector. In this way we can add the same vector to many points, as illustrated in the image bellow. The vectors you see are all the same, but the points resulting from adding it to a group of existing points in different locations all differ.

Calculating with Vectors

As shown by the simple examples above, the power of vectors really comes into play when we use them in mathematical calculations, treating them as if they were simple values. Here an overview of the different possible operations.

Vector Addition and Subtraction

A vector can be added to another, and the result is the same as if we superposed two descriptions of how to get from one place to another, resulting in a third vector.

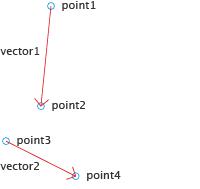
We start with four points:

var point1 = new Point(50, 0);
var point2 = new Point(40, 100);

var point3 = new Point(5, 135);
var point4 = new Point(75, 170);

As seen in Points and Vectors, we can now calculate the two vectors by subtracting the points from each other:

var vector1 = point2 - point1;
// = { x: 40, y: 100 } - { x: 50, y: 0 }
// = { x: -10, y: 100 }

var vector2 = point4 - point3;
// = { x: 75, y: 170 } - { x: 5, y: 135 }
// = { x: 70, y: 35 }

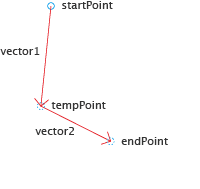
To start at startPoint, follow vector1 and then vector2, we could first add vector1 to the startPoint, retrieve the resulting tempPoint and then add vector2 to that to get to the desired endPoint.

var tempPoint = startPoint + vector1;
var endPoint = tempPoint + vector2;

But if we would like to apply the same combined vector to many points, this calculation would be unnecessarily complicated, as we would have to go through the tempPoint each time.

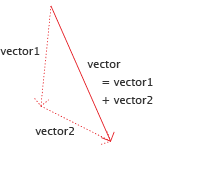
Instead, we can just add vector1 to vector2 and use the resulting object as a new vector that describes the combined movement.

var vector = vector1 + vector2;

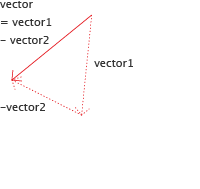
But we can also do the opposite and subtract a vector from another instead of adding it. The result is the same as if we would go in the opposite direction of the vector that we are subtracting.

var vector = vector1 - vector2;

Vector Multiplication and Division

It is quite easy to imagine what a multiplication or division with a numerical value would do to a vector: Instead of saying "go 10 meters into that direction", it would for example correspond to "3 times 10 meters into that direction". A multiplied vector does not change its angle. But its length is changed, by the amount of the multiplied value.

var bigVector = smallVector * 3;

Or, to go the other way:

var smallVector = bigVector / 3;

var bigVector = 3 * smallVector;

Changing a Vector's Length

So we learned that multiplying or dividing a vector changes its length without modifying its angle. But we can also change the length property on vector objects directly:

First we create a vector by directly use the Point constructor, since vectors and points are actually the same type of objects:

var vector = new Point(24, 60);
print(vector.length);
// 64.62198

Now we change the vector's length property. This is similar to the multiplication in the previous example, but modifies the object directly:

vector.length = vector.length * 3;
print(vector.length);
// 193.86593

We can also set the length to a fixed value, stretching or shrinking the vector to this length:

vector.length = 100;

Another way to change the vector's length is the point.normalize() method. In Mathematics to normalize a vector means to resize it so its length is 1. normalize() handles that for us, and also accepts an optional parameter that defines the length to normalize to, if we would like it to be other than 1.

We start with the same vector as in the example above on line 1. Let's look at the normalized version of this vector:

var vector = new Point(24, 60); 
var normalizedVector = vector.normalize();
print(vector.length);
// 64.62198
print(normalizedVector.length);
// 1

Note that the length of normalizedVector is now 1, while the original vector remains unmodified. normalize() does not modify the vector it is called on, instead it returns a new normalized vector object.

Now what happens if we normalize to 10 instead?

var normalizedVector = vector.normalize(10);
print(normalizedVector.length);
// 10

As expected, the returned vector has a length of 10. Note that we could also multiply the first normalized vector with 10:

var normalizedVector = vector.normalize() * 10;
print(normalizedVector.length);
// 10

Rotating Vectors and Working with Angles

Rotating vectors is a powerful tool for constructing paths and shapes, as it allows us to define a relative direction at a certain angle rotated away from another direction, for example sideways. The tutorial Working with Mouse Vectors show a good example of this, where rotated vectors are used to construct paths in parallel to the direction and position of the moved mouse.

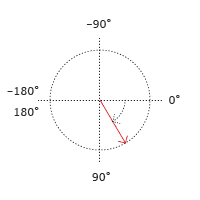
All angles in Scriptographer are measured in degrees, and are oriented clockwise. The angle values start from the horizontal axis and expand downwards. At 180° they flip to -180°, which is the same, since going halfway around a circle in the left or right direction results in the same position. This does not prevent you from setting angles to something higher than 180° though.

Please note:

If you set the script.coordinateSystem property to 'bottom-up' and therefore flip the coordinate system vertically, the orientation of angles also changes and their orientation becomes counter-clockwise. Read more about this setting in the tutorial about The Coordinate System

There are two ways to change the angle of a vector. The obvious one is by setting the vector's angle property to a new value. Let's first set up a vector that points 100 coordinates down and 100 to the right, and print its angle and length:

var vector = new Point(100, 100);
print(vector.angle);
// 45

Since we are going in equal amounts down and to the right, it has an angle of 45°. Let's print it's length so we can check it after we have rotated the vector:

print(vector.length);
// 141.42136

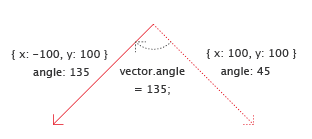
Now we rotate it by 90° clockwise by setting its angle to 45° + 90° = 135° and print the length again:

vector.angle = 135;
print(vector.length);
// 141.42136

Note how the length has not changed. All we changed is the vector's direction. If we print the whole vector again, we will see that its coordinates are not the same anymore:

print(vector);
// { x: -100, y: 100 }

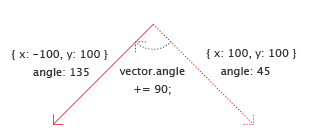
Instead of setting the angle directly to 135, we could have also explicitly increase it by 90°:

vector.angle = vector.angle + 90;

A simpler way of writing such an increase of a value is to use the += operator, as it prevents us from writing vector.angle twice:

vector.angle += 90;

script.angleUnits = 'radians';

Operations, Methods and Properties

Note that mathematical operations (addition, subtraction, multiplication and division) and methods such as rotate() and normalize() do not modify the involved vector and point objects. Instead, they return the result as a new object. This means they can be chained and combined in expressions:

var point = event.middlePoint
		+ event.delta.rotate(90);

Changing a vector's angle or length on the other hand directly modifies the vector object, and can only be used outside of such expressions. Since we are directly modifying objects, we need to be careful about what we modify and use the clone() function when the original object shall not be modified.

var delta = event.delta.clone();
delta.angle += 90;
var point = event.middlePoint + delta;

Vektor.js

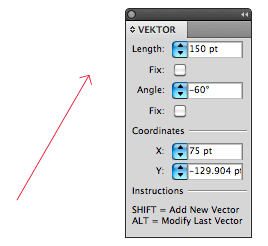
In the Examples/Tools folder you can find the didactic Vektor.js tool. It is provided as a help to familiarise yourself with the concept of vectors.

Play around with it to get a feeling for how vectors work, and try to use it to repeat the principles learned in this tutorial.